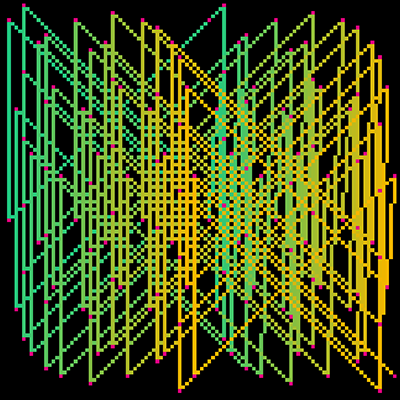
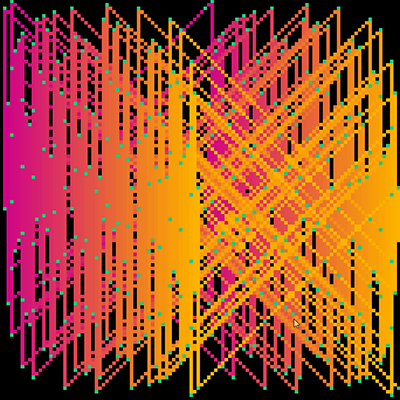
presented here are some images from a collaboration between myself and Robert Voorheis, a close friend and mathematician. Together, we devised and created a novel three-dimensional expression of modular arithmetic, the same kind of math logic that governs how a clock is read (modulo 12).
the project was accepted as an exhibition at the 2018 Bridges Conference Mathematical Art Galleries. From our submission documents:
"A visualization of a 3D graph in which each vertex lies on a three-dimensional integer lattice. The set of vertices defining the graph is precisely the set of points (x, y, z) such that x*y*z ≡ 7 modulo 17. The set of vertices has tetrahedral symmetry; that is, they can be separated into 4 distinct quadrants which can be permuted analogously to the 4 vertices of a regular tetrahedron. This visualization of modular multiplication reveals a unexpectedly pleasing geometric structure that appears simultaneously randomized and highly-structured."
later, in Fall 2019, I further developed the concept by making a series of 2D pixel-art paintings based on the same equations.